3) Multinomial Logistic Regression - Softmax
: 여러 개의 클래스를 예측하는 데 사용되는 확률적 분류 모델. 이 모델은 각 클래스에 대한 확률을 계산하고, 입력 특성의 가중치와 편향을 사용하여 이러한 확률을 추정
<특징>
- Logistic 함수를 사용하여 클래스별 확률을 추정한다. 로지스틱 함수는 입력 변수의 선형 조합을 취하여 0과 1 사이의 확률 값을 출력하는 함수이다
- Softmax 함수는 로지스틱 함수의 확장으로, 입력 변수의 선형 조합을 취하여 여러 클래스에 대한 확률 분포를 계산한다. 이 함수는 각 클래스에 대한 확률을 정규화하여 합이 1이 되도록 만든다
- 모델을 학습하기 위해서는 손실 함수를 최소화해야 한다. 따라서 Li=-log(pj)를 해서 pj를 최대화하면 Li가 최소화되는 것MLR에서는 Cross-Entropy 손실 함수를 사용한다.
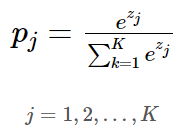
K는 클래스 수를 나타내며, 는 SoftMax 함수의 입력값이다. 해석하면 (으로 볼 수 있다.
지수함수는 미분하기 위함이며 입력값 중 큰 값은 더 크게, 작은 값은 더 작게 만들어 입력벡터가 더 잘 구분되게 하기 위함이다.
<붓꽃 문제> - iris 데이터를 이용한 다중 클래스 분류 모델을 만드는 문제

1. 소프트맥스 함수의 입력으로 어떻게 바꿀까?
데이터는 4개의 독립변수를 가지는데 이는 모델이 4차원 벡터를 입력으로 받음을 의미한다.
그런데 소프트맥스 함수의 입력으로 사용되는 벡터의 차원은 분류하고자 하는 클래스의 개수(붓꽃 종류)가 되어야 하므로 가중치 연산을 통해 3차원 벡터로 변환되어야 한다. z는 소프트맥스 함수의 입력으로 사용되는 3차원 벡터이다.

softmax 함수의 입력 벡터 z의 차원수만큼 결과값이 나오도록 가중치를 곱한다
위의 그림에서 화살표는 총 (4 x 3 = 12) 12개이며 전부 다른 가중치를 가지고, 학습 과정에서 점차적으로 오차를 최소화하는 가중치로 값이 업데이트된다
2. 오차는 어떻게 구할까?
softmax 함수의 출력은 벡터로 각 원소는 0과 1사이의 값을 가지며, 이 각각은 특정 클래스가 정답일 확률을 나타낸다.
즉, 은 virginica가 정답일 확률, 2는 setosa가 정답일 확률, 3은 versicolor가 정답일 확률을 의미한다.
이제 이 예측값과 비교할 수 있는 실제값의 표현 방법이 있어야 한다. softmax 회귀에서는 실제 원-핫 벡터로 표현한다
(원-핫 벡터: 그냥 분류하려고 1 나머지는 0으로 표현하는 것)

데이터의 실제값이 setosa라면, setosa의 원-핫 벡터는 [0 1 0]이다. 이 경우, 예측값과 실제값의 오차가 0이 되려면 softmax 함수의 결과가 [0 1 0]이 되야 한다.
이 두 벡터 [0.26 0.70 0.04] [0 1 0] 의 오차를 계산하기 위해서 softmax 회귀는 손실함수로 cross-entropy 함수를 사용한다.

이후 손실함수가 최소가 되는 방향으로 가중치를 update 한다
cross entropy가 뭐지?
예측 모형은 실제 분포인 q 를 모르고, 모델링을 하여 q 분포를 예측하고자 한다. 예측 모델링을 통해 구한 분포를 p(x) 라고 하자 실제 분포인 q를 예측하는 p 분포를 만들었을 때, cross-entropy는 다음과 같다

ex) 가방에 0.8/0.1/0.1 의 비율로, 빨간/녹색/노랑 공이 들어가 있다
하지만 직감에는 0.2/0.2/0.6의 비율로 들어가 있을 것 같다. 이 때, entropy 와 cross-entropy 는 아래와 같이 계산된다

cross entropy를 이용한 loss function
이미지를 읽어들여 virginica / setosa / versicolor 3개의 클래스를 갖는 다중 분류 문제를 생각해보자.
가방에 virginica / setosa / versicolor 라고 쓰인 공이 있다. 이 공에 해당 이미지에 대한 정답을 사람이 적어 놓았다.
예측 모형은 주어진 정보 (이미지) 를 살펴본 후, 예측 분포를 산출했는데, p(y) = [0.2, 0.3, 0.5] 으로 예측했다.
즉, 공 (실제 정답) 을 꺼냈을 때, virginica / setosa / versicolor 를 관찰할 확률이 각각 0.2/0.3/0.5 일 것이라고 예측했다
하지만 실제 분포, q(y) = [0, 0, 1] 이다. 이 때, cross-entropy 는 매우 간단하게, -log(0.5) 이다.
현실의 분류 문제에서는 정답이 있다고 가정하고 하기 때문에 실제 분포인 q(y)가 [0,0,1], [1,0,0] .. 과 같은 one-hot encoding 된 벡터로 나타내어진다. 왜냐하면 실제 이미지가 0.2 의 확률로 나타낼 수는 없기 때문이다. 하지만 cross-entropy 는 p와 q에서 정의되는 것이므로 구할 수 있다.

보통 초기의 W는 매우 작다 따라서 s는 0과 가깝다 그러면 Li 값이 1이 되고 class가 3개 이므로 각각 1/3 1/3 1/3의 loss를 가지게 된다
SVM과 SoftMax의 비교
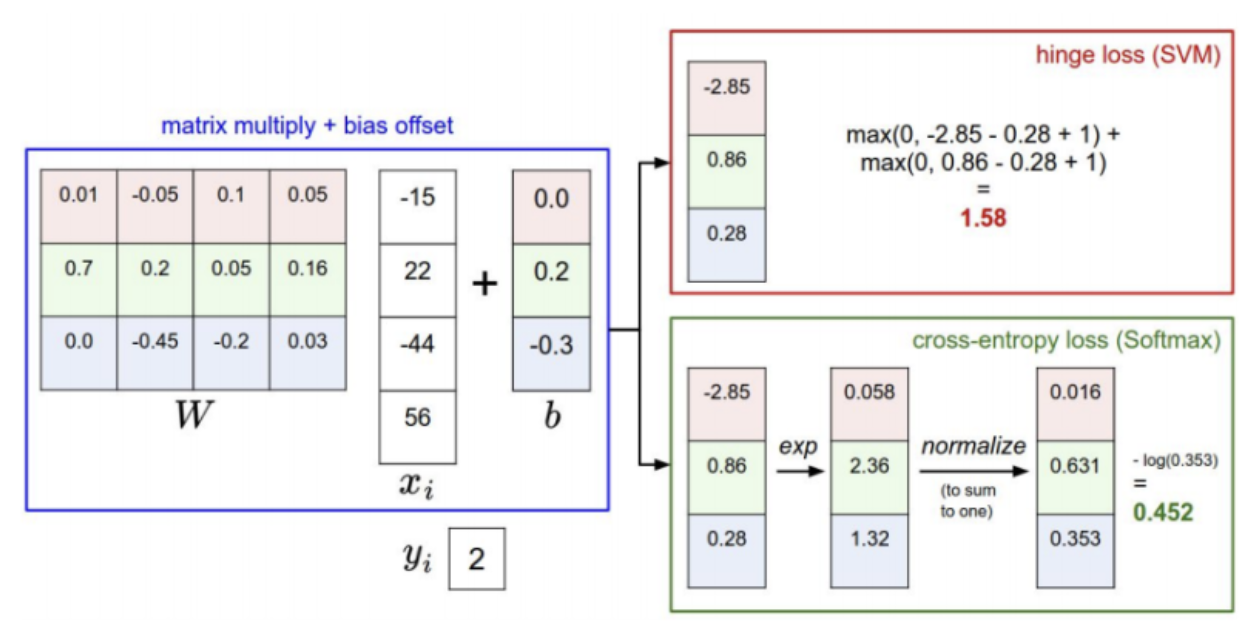
-SVM
W와 xi 곱하고 b를 더하니 (3x4 와 4x1 + 3x1 = 3x1) -> -2.85 0.86 0.28 도출
파란색을 ground truth class로 보고 있어서 0.28을 syi로 하면 계산 결과 1.58 나옴
-SoftMax
-2.85 0.86 0.28 을 exponential하고 normalize한 결과임
ground truth class 0.353 대입결과 0.452 도출됨
예제) data의 score을 조금씩 변형 함

SVM에서 +1을 해주는 margin을 통해 robustness을 주고 있음 따라서 loss값 불변
SoftMax에서는 모든 인자들을 반영하기 때문에 변함
'CS231n' 카테고리의 다른 글
| CS231n(4) Introduction to Neural Networks (0) | 2024.03.04 |
|---|---|
| CS231n(3-3) Loss Functions and Optimization (0) | 2024.02.22 |
| CS231n(3-1) Loss Functions and Optimization (0) | 2024.02.15 |
| CS231n(2) Image Classification (0) | 2024.02.14 |
| CS231n(1) Introduction to Convolutional Neural Networks for Visual Recognition (1) | 2024.02.14 |



